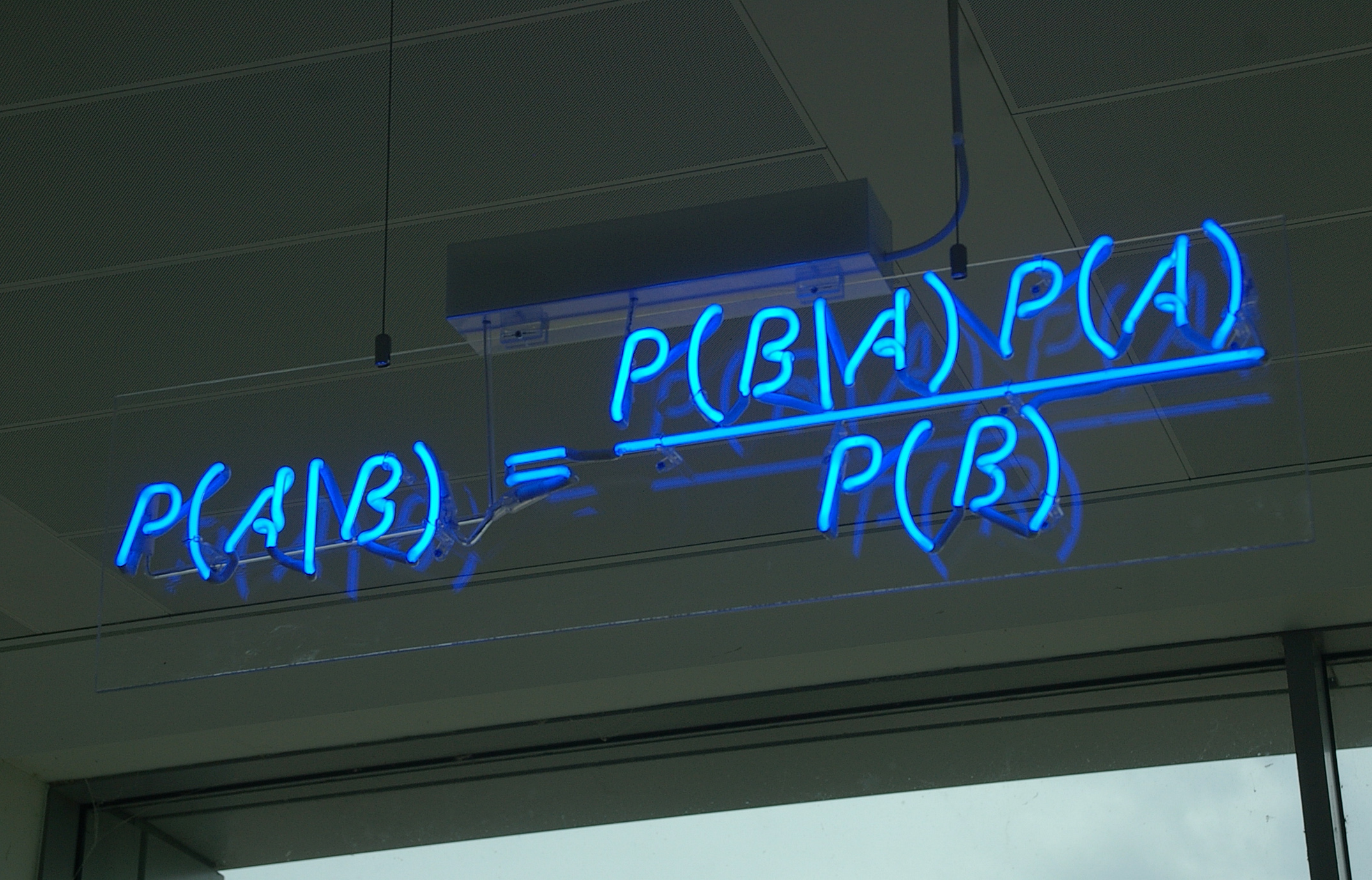This is an outline for a talk I gave at Bar Camp Boston 8 on the automation of science. It's a topic I've blogged and spoken about before. The shortened URL for this post is http://goo.gl/rv3Xik.
In 2004, a robot named Adam became the first machine in history to discover new scientific knowledge independently of its human creators. Without human guidance, Adam can create hypotheses to explain observations, design experiments to test those hypotheses, run the experiments using laboratory robotics, interpret the experimental results, and repeat the cycle to generate new knowledge. The principal investigator on the Adam project was Ross King, now at Manchester University, who published a paper on the automation of science (PDF) in 2009. Some of his other publications: 1, 2, 3.
Adam works in a very limited domain, in nearly complete isolation. There is plenty of laboratory automation but (apart from Adam) we don't yet have meaningful computer participation in the theoretical aspect of scientific work. A worldwide scientific collaboration of human and computer theoreticians working with human and computer experimentalists could advance science and medicine and solve human problems faster.
The first step is to formulate a linked language of science that machines can understand. Publish papers in formats like RDF/Turtle or JSON or JSON-LD or YAML. Link scientific literature to existing semantic networks (DBpedia, Freebase, Google Knowledge Graph, LinkedData.org, Schema.org etc). Create schemas for scientific domains and for the scientific method (hypotheses, predictions, experiments, data). Provide tutorials, tools and incentives to encourage researchers to publish machine-tractable papers. Create a distributed graph or database of these papers, in the role of scientific journals, accessible to people and machines everywhere. Maybe use Stackoverflow as a model for peer review.
Begin with very limited scientific domains (high school physics, high school chemistry) to avoid the full complexity and political wrangling of the professional scientific community in the initial stages. As this stuff approaches readiness for professional work, deploy it first in the domain of computer science and other scientific domains where it can hope to avoid overwhelming resistance.
Machine learning algorithms (clustering, classification, regression) can find patterns in data and help to identify useful abstractions. Supervised learning algorithms can provide tools of collaboration between people and computers.
The computational chemistry folks have a cool little program called Babel which translates between a large number of different file formats for representing molecular structures. It does this with a rich internal representation of structures, and pluggable read and write modules for each file format. At some point, something like this for different file formats of scientific literature might become useful, and might help to build consensus among different approaches.
A treasure trove would be available in linked patient data. In the United States this is problematic because of the privacy restrictions associated with HIPAA regulation. In countries like Iceland and Norway which have universal health care, there would be no equivalent of HIPAA, and those would be good places to initiate a Linked Patient Data project.
In 2004, a robot named Adam became the first machine in history to discover new scientific knowledge independently of its human creators. Without human guidance, Adam can create hypotheses to explain observations, design experiments to test those hypotheses, run the experiments using laboratory robotics, interpret the experimental results, and repeat the cycle to generate new knowledge. The principal investigator on the Adam project was Ross King, now at Manchester University, who published a paper on the automation of science (PDF) in 2009. Some of his other publications: 1, 2, 3.
Adam works in a very limited domain, in nearly complete isolation. There is plenty of laboratory automation but (apart from Adam) we don't yet have meaningful computer participation in the theoretical aspect of scientific work. A worldwide scientific collaboration of human and computer theoreticians working with human and computer experimentalists could advance science and medicine and solve human problems faster.
The first step is to formulate a linked language of science that machines can understand. Publish papers in formats like RDF/Turtle or JSON or JSON-LD or YAML. Link scientific literature to existing semantic networks (DBpedia, Freebase, Google Knowledge Graph, LinkedData.org, Schema.org etc). Create schemas for scientific domains and for the scientific method (hypotheses, predictions, experiments, data). Provide tutorials, tools and incentives to encourage researchers to publish machine-tractable papers. Create a distributed graph or database of these papers, in the role of scientific journals, accessible to people and machines everywhere. Maybe use Stackoverflow as a model for peer review.
Begin with very limited scientific domains (high school physics, high school chemistry) to avoid the full complexity and political wrangling of the professional scientific community in the initial stages. As this stuff approaches readiness for professional work, deploy it first in the domain of computer science and other scientific domains where it can hope to avoid overwhelming resistance.
Machine learning algorithms (clustering, classification, regression) can find patterns in data and help to identify useful abstractions. Supervised learning algorithms can provide tools of collaboration between people and computers.
The computational chemistry folks have a cool little program called Babel which translates between a large number of different file formats for representing molecular structures. It does this with a rich internal representation of structures, and pluggable read and write modules for each file format. At some point, something like this for different file formats of scientific literature might become useful, and might help to build consensus among different approaches.
A treasure trove would be available in linked patient data. In the United States this is problematic because of the privacy restrictions associated with HIPAA regulation. In countries like Iceland and Norway which have universal health care, there would be no equivalent of HIPAA, and those would be good places to initiate a Linked Patient Data project.